Formula generator for CONFIDENCE.T FUNCTION function
The CONFIDENCE.T function is used to calculate the width of half the confidence interval for a Student's t-distribution. It takes three arguments: alpha, which represents the significance level; standard_deviation, which is the standard deviation of the population; and size, which is the sample size. The function returns the width of half the confidence interval.
Formula generator
Spreadsheet AI is the #1 AI for generating and comprehending Excel and Google Sheets formulas. With its advanced capabilities, it goes beyond the basics by providing support for VBA and custom tasks. Streamline your spreadsheet with Spreadshee AI
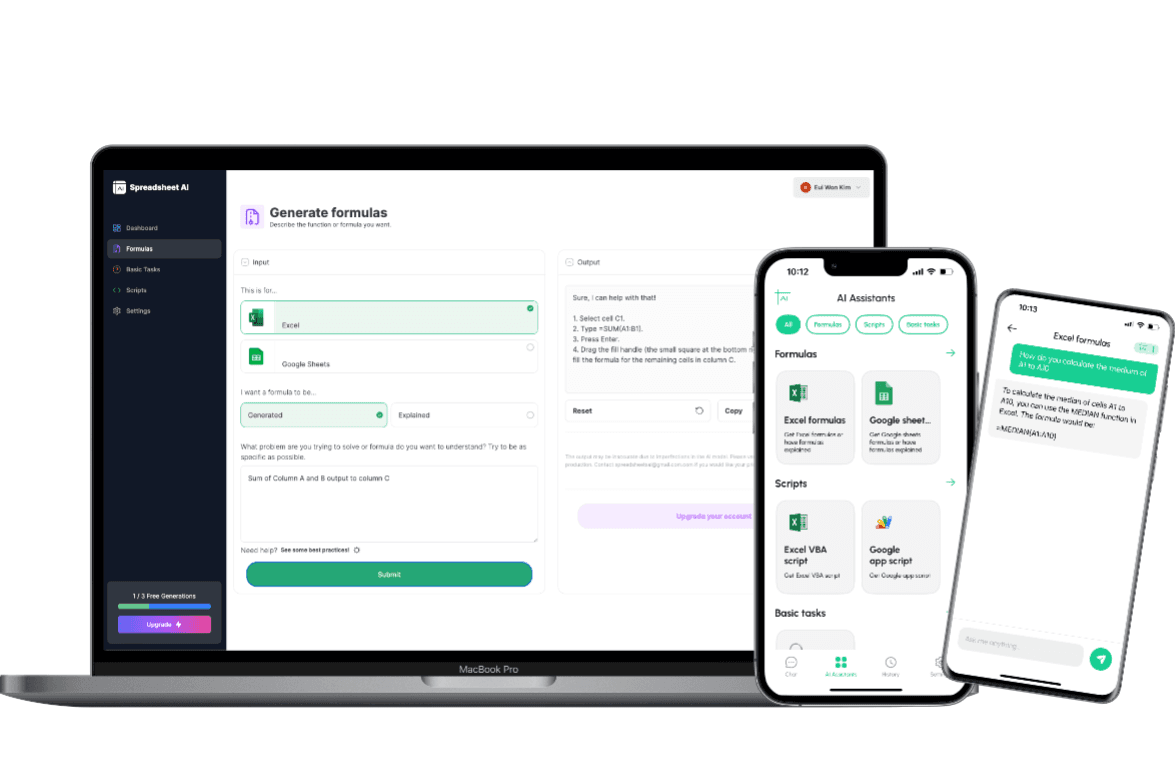
How to generate an CONFIDENCE.T FUNCTION formula using AI.
To obtain information on the ARRAY_CONSTRAIN formula, you could ask the AI chatbot the following question: “To obtain the CONFIDENCE.T formula from an AI chatbot, you could ask: "What is the formula for calculating the confidence interval for a given sample mean, without knowing about CONFIDENCE.T in Excel?"”
CONFIDENCE.T FUNCTION formula syntax
The CONFIDENCE.T function in Excel is used to calculate the confidence interval for a population mean, based on a sample. The syntax for the CONFIDENCE.T function is as follows: CONFIDENCE.T(alpha, standard_dev, sample_size) - alpha: This is the significance level or the desired level of confidence. It is typically a value between 0 and 1, representing the probability of obtaining a confidence interval that contains the true population mean. - standard_dev: This is the standard deviation of the population. If the standard deviation is unknown, you can estimate it using the sample standard deviation. - sample_size: This is the size of the sample that you are working with. The CONFIDENCE.T function returns the margin of error, which is the amount by which the sample mean is likely to differ from the true population mean. It is calculated as the product of the standard error (standard_dev / sqrt(sample_size)) and the appropriate t-value from the Student's t-distribution. Note that the CONFIDENCE.T function assumes that the sample is drawn from a normally distributed population.
Use Cases & Examples
In these use cases, we use the CONFIDENCE.T function to calculate the confidence interval for a population mean, given a sample mean, sample size, and desired level of confidence.
Calculating Confidence Interval Width
Description
In this use case, we use the CONFIDENCE.T function to calculate the width of half the confidence interval for a Student's t-distribution. The function takes three arguments: alpha, which represents the significance level; standard_deviation, which is the standard deviation of the population; and size, which is the sample size. The function returns the width of half the confidence interval.
Result
CONFIDENCE.T(alpha, standard_deviation, size)
Estimating Sample Size
Description
In this use case, we use the CONFIDENCE.T function to estimate the required sample size for a given confidence level and margin of error. The function takes three arguments: alpha, which represents the significance level; standard_deviation, which is the standard deviation of the population; and margin_of_error, which is the desired margin of error. The function returns the required sample size to achieve the desired confidence level and margin of error.
Result
CONFIDENCE.T(alpha, standard_deviation, margin_of_error)
Testing Hypotheses
Description
In this use case, we use the CONFIDENCE.T function to test hypotheses about the mean of a population. The function takes three arguments: alpha, which represents the significance level; standard_deviation, which is the standard deviation of the population; and size, which is the sample size. The function returns the confidence interval for the mean of the population. By comparing the confidence interval to a hypothesized value, we can determine if the null hypothesis should be rejected or not.
Result
CONFIDENCE.T(alpha, standard_deviation, size)
AI tips
Enhance Your Excel Efficiency with AI Tips: Discover our innovative Excel add-in feature, ‘AI Tips.’ Streamline your workflow and boost productivity as AI-powered suggestions offer real-time insights for optimal spreadsheet organization, data analysis, and visualization. Elevate your Excel experience with intelligent recommendations tailored to your unique needs, helping you work smarter and achieve more.
Provide Clear Context
When describing your requirements to the AI, provide clear and concise context about the data you have, the specific task you want to accomplish, and any relevant constraints or conditions. This helps the AI understand the problem accurately.
Include Key Details
Include important details such as column names, data ranges, and specific criteria that need to be considered in the formula. The more precise and specific you are, the better the AI can generate an appropriate formula.
Use Examples
If possible, provide examples or sample data to illustrate the desired outcome. This can help the AI better understand the pattern or logic you are looking for in the formula.
Mention Desired Functionality
Clearly articulate the functionality you want the formula to achieve. Specify if you are looking for lookups, calculations, aggregations, or any other specific operations.
FAQ
Frequently Asked Questions
- The CONFIDENCE.T function calculates the confidence interval for a population mean, using a Student's t-distribution.
- To use the CONFIDENCE.T function, you need to provide the significance level (alpha) and the standard deviation of the population. The formula is CONFIDENCE.T(alpha, standard_dev, sample_size).
- The significance level (alpha) is the probability of making a Type I error, which is rejecting the null hypothesis when it is actually true. Common values for alpha are 0.05 or 0.01.
- The standard deviation of the population is a measure of the variability of the data points in the entire population. If you don't have the population standard deviation, you can use the sample standard deviation as an estimate.
- The sample size is the number of observations or data points in your sample. It should be a positive integer.